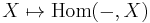Functor category

In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors. Functor categories are of interest for two main reasons:

• many commonly occurring categories are (disguised) functor categories, so any statement proved for general functor categories is widely applicable;
• every category embeds in a functor category (via the Yoneda embedding); the functor category often has nicer properties than the original category, allowing certain operations that were not available in the original setting.

Contents 1 Definition 2 Examples 3 Facts 4 See also 5 References

Definition

Suppose C is a small category (i.e. the objects and morphisms form a set rather than a proper class) and D is an arbitrary category. The category of functors from C to D, written as Funct(C,D) or D^C, has as objects the covariant functors from C to D, and as morphisms the natural transformations between such functors. Note that natural transformations can be composed: if μ(X) : F(X) → G(X) is a natural transformation from the functor F : C → D to the functor G : C → D, and η(X) : G(X) → H(X) is a natural transformation from the functor G to the functor H, then the collection η(X)μ(X) : F(X) → H(X) defines a natural transformation from F to H. With this composition of natural transformations (known as vertical composition, see natural transformation), D^C satisfies the axioms of a category.

In a completely analogous way, one can also consider the category of all contravariant functors from C to D; we write this as Funct(C^op,D).

If C and D are both preadditive categories (i.e. their morphism sets are abelian groups and the composition of morphisms is bilinear), then we can consider the category of all additive functors from C to D, denoted by Add(C,D).

Examples

• If I is a small discrete category (i.e. its only morphisms are the identity morphisms), then a functor from I to C essentially consists of a family of objects of C, indexed by I; the functor category C^I can be identified with the corresponding product category: its elements are families of objects in C and its morphisms are families of morphisms in C.
• A directed graph consists of a set of arrows and a set of vertices, and two functions from the arrow set to the vertex set, specifying each arrow's start and end vertex. The category of all directed graphs is thus nothing but the functor category Set^C, where C is the category with two objects connected by two morphisms, and Set denotes the category of sets.
• Any group G can be considered as a one-object category in which every morphism is invertible. The category of all G-sets is the same as the functor category Set^G.
• Similar to the previous example, the category of k-linear representations of the group G is the same as the functor category k-Vect^G (where k-Vect denotes the category of all vector spaces over the field k).
• Any ring R can be considered as a one-object preadditive category; the category of left modules over R is the same as the additive functor category Add(R,Ab) (where Ab denotes the category of abelian groups), and the category of right R-modules is Add(R^op,Ab). Because of this example, for any preadditive category C, the category Add(C,Ab) is sometimes called the "category of left modules over C" and Add(C^op,Ab) is the category of right modules over C.
• The category of presheaves on a topological space X is a functor category: we turn the topological space into a category C having the open sets in X as objects and a single morphism from U to V if and only if U is contained in V. The category of presheaves of sets (abelian groups, rings) on X is then the same as the category of contravariant functors from C to Set (or Ab or Ring). Because of this example, the category Funct(C^op, Set) is sometimes called the "category of presheaves of sets on C" even for general categories C not arising from a topological space. To define sheaves on a general category C, one needs more structure: a Grothendieck topology on C. (Some authors refer to categories that are equivalent to Set^C as presheaf categories.^[1])

Facts

Most constructions that can be carried out in D can also be carried out in D^C by performing them "componentwise", separately for each object in C. For instance, if any two objects X and Y in D have a product X×Y, then any two functors F and G in D^C have a product F×G, defined by (F×G)(c) = F(c)×G(c) for every object c in C. Similarly, if η_c : F(c)→G(c) is a natural transformation and each η_c has a kernel K_c in the category D, then the kernel of η in the functor category D^C is the functor K with K(c) = K_c for every object c in C.

As a consequence we have the general rule of thumb that the functor category D^C shares most of the "nice" properties of D:

• if D is complete (or cocomplete), then so is D^C;
• if D is an abelian category, then so is D^C;

We also have:

• if C is any small category, then the category Set^C of presheaves is a topos.

So from the above examples, we can conclude right away that the categories of directed graphs, G-sets and presheaves on a topological space are all complete and cocomplete topoi, and that the categories of representations of G, modules over the ring R, and presheaves of abelian groups on a topological space X are all abelian, complete and cocomplete.

The embedding of the category C in a functor category that was mentioned earlier uses the Yoneda lemma as its main tool. For every object X of C, let Hom(-,X) be the contravariant representable functor from C to Set. The Yoneda lemma states that the assignment

is a full embedding of the category C into the category Funct(C^op,Set). So C naturally sits inside a topos.

The same can be carried out for any preadditive category C: Yoneda then yields a full embedding of C into the functor category Add(C^op,Ab). So C naturally sits inside an abelian category.

The intuition mentioned above (that constructions that can be carried out in D can be "lifted" to D^C) can be made precise in several ways; the most succinct formulation uses the language of adjoint functors. Every functor F : D → E induces a functor F^C : D^C → E^C (by composition with F). If F and G is a pair of adjoint functors, then F^C and G^C is also a pair of adjoint functors.

The functor category D^C has all the formal properties of an exponential object; in particular the functors from E × C → D stand in a natural one-to-one correspondence with the functors from E to D^C. The category Cat of all small categories with functors as morphisms is therefore a cartesian closed category.

See also

• Diagram (category theory)

References